Una Aplicación no tan Conocida de la Transformada de Fourier
La transformada de Fourier es una herramienta matemática ampliamente utilizada en distintos campos de las matemáticas, física e ingeniería. Esta herramienta permite una visualización alternativa, en el dominio transformado (comúnmente denominado como frecuencia), de una determinada señal que varíe en el tiempo o en el espacio [1], lo cual es particularmente útil cuando es difícil analizar o procesar directamente la señal original. Véase como ejemplo la Figura 1, donde una señal compleja y difícil de tratar en tiempo es muy fácil de analizar en su dominio transformado de frecuencia.
El uso más popular de la transformada de
Fourier lo podemos encontrar en la industria musical, en la composición, descomposición,
filtrado y mezclado de señales de audio que se realiza en estudios de grabación
[2]. Sin embargo, hay multitud de campos que también se benefician de su uso,
como las telecomunicaciones o la óptica. De hecho, hay una rama completa
de la óptica, denominada Óptica de Fourier, que se fundamenta en su uso. Dentro
del grupo de investigación SWAT, es común la aplicación de esta herramienta en
trabajos de diversa índole, desde la caracterización de canales de propagación
[3] hasta el análisis de metamateriales y estructuras periódicas [4].
Sin embargo, hay una aplicación de la transformada de Fourier que, aunque de gran utilidad, no es tan común de encontrar resaltada en libros de texto. La transformada de Fourier puede utilizarse para calcular la derivada de una determinada función, tanto de forma analítica como numérica. El método de lo que denominaremos la derivada de Fourier es particularmente útil en la resolución de ecuaciones en derivadas parciales, lo cual tiene aplicación directa en la comprensión de multitud de efectos asociados con transferencia de calor [5], propagación de ondas electromagnéticas y acústicas en un medio [6], etc.
Figura
1. Señal en tiempo y su espectro en frecuencia obtenido con la transformada
de Fourier. Imagen extraída de [2].
Un Poco de Matemáticas
Una de las propiedades que se deducen de la aplicación de propiedades algebraicas básicas sobre la Transformada de Fourier atañe a la derivada de una determinada función f. Se puede demonstrar fácilmente (véase [7]), que la transformada de Fourier, F{·}, de una derivada de primer orden es igual a la transformada de Fourier de la propia función multiplicada por un término jw (j es la unidad imaginaria y w es la frecuencia angular). Matemáticamente se puede expresar como
La expresión anterior es generalizable a
derivadas de mayor orden (de orden n) según la siguiente ecuación:
De este modo, tenemos una manera alternativa y eficiente de calcular la derivada de una determinada función. De hecho, la expresión anterior permite calcular derivadas fraccionales de una manera sencilla, es decir, derivadas cuyo orden no es un número entero (por ejemplo, la “media derivada” donde n=0.5). Las exóticas derivadas fraccionales o, en general, el denominado cálculo fraccional, tiene aplicaciones prácticas en diversos campos como la física, la ingeniería o la biología [8]. Una curiosa aplicación de las derivadas fraccionales se encuentra en la detección de hipertrofias cardíacas [9].
Programando la Derivada de una Función con el Método de
Fourier
Con tan solo unas pocas líneas de código, es sencillo calcular en cualquier lenguaje de programación una derivada con el método de Fourier [10]. Además, el cálculo es bastante eficiente en términos computacionales, al hacer uso de la transformada rápida de Fourier (FFT) y su asociada transformada rápida inversa (IFFT). Nótese que los algoritmos FFT e IFFT reducen el coste computacional de una transformada de Fourier de un orden O(N^2) a O(N logN). La reducción de tiempo en cálculo es muy significativa a medida que el número de muestras N aumenta.
La Figura 2 muestra un ejemplo de programación de la derivada de Fourier en el lenguaje de programación Matlab, lenguaje ampliamente utilizado por la comunidad de ingenieros. En este caso, intentaremos calcular la primera derivada (orden n=1) de la función sinc(t), que se define como el cociente de la función seno y la variable temporal t:
Para ello, creamos un array equiespaciado de tiempos t, que posee N=150 muestras y que varía entre -L/2 = -50 segundos y L/2 = 50 segundos.
En las líneas 17 y 18 del código Matlab calculamos la derivada numérica con las expresiones matemáticas vistas en la sección anterior y el uso de las transformadas rápidas de Fourier: directa (FFT, de tiempo a frecuencias) e inversa (IFFT, de frecuencias a tiempo). Aunque a nivel analítico trabajamos con valores reales de la variable t y, por tanto, la función f(t) es siempre real, a nivel numérico pueden quedar pequeños rastros espurios de valores complejos posteriores a la aplicación del comando IFFT. Podemos eliminar fácilmente estos valores espurios quedándonos con la parte real de la derivada, que es lo que hacemos en la línea 21 del código Matlab.
Para más información de cómo programar el
mismo método en el lenguaje de programación Python (paquete “numpy”), es
recomendable ver [11].
Figura
2. Código de Matlab para calcular derivadas con el método de la transformada de
Fourier.
Ejemplos Prácticos
A continuación, se muestra un ejemplo práctico
del cálculo numérico de la derivada de la función sinc(t) por el método de la
transformada de Fourier. Para comparar la validez del método, también mostramos
la derivada analítica de la función. La derivada analítica se puede calcular aplicando
la regla de la derivada de un cociente, resultando en
Por otro lado, el método
de diferencias finitas busca aproximar la derivada por una serie de
ecuaciones en diferencias, es decir, por una serie de restas y cocientes
que involucran a los valores de la función considerada. El esquema de
diferencias progresivas (en inglés, forward), se puede representar
matemáticamente como
La Figura 3 muestra una comparativa entre la
solución analítica (círculos negros), el método de Fourier (línea roja) y un
método progresivo de diferencias finitas (línea azul) para el cálculo de la
derivada de la función sinc(t). Tal y como se puede observar, la
correspondencia entre los dos métodos numéricos y la solución analítica es muy
buena.
Figura
3. Cálculo de la derivada de la función sinc(t). En círculos negros, solución
analítica. En rojo, método de la transformada de Fourier. En azul, método de
diferencias finitas.
Aunque
en la Figura 3 no se puede apreciar directamente, el método de la derivada de
Fourier ofrece, en términos generales, resultados más precisos que el de diferencias
finitas. Por este motivo, para implementaciones más complejas que involucren a
variables temporales y espaciales (por ejemplo, ecuaciones en derivadas
parciales), se pueden aplicar métodos mixtos que combinan diferencias finitas
en tiempo y métodos de Fourier en espacio, con el objetivo de mejorar la
precisión de la solución obtenida. En [12, minuto 8’ 35”] se muestra un ejemplo
gráfico de lo anteriormente comentado.
La
Figura 4 muestra una comparativa entre la convergencia en Matlab de los métodos
de Fourier (línea roja) y de diferencias finitas (línea azul), para el cálculo de
la derivada de la función sinc(t), a medida que el número de muestras
utilizadas N aumenta. Tal y como se puede apreciar, el método espectral
de Fourier converge mucho más rápido (el error es menor) cuando se utiliza un
número pequeño de muestras N. Esto se debe al hecho de que el error en el
método de diferencias finitas es directamente proporcional al valor del paso de
tiempo utilizado (mientras más pequeño es, menor es el error en la estimación).
A cambio, el coste computacional del método expuesto de diferencias finitas es
de orden O(N) mientras que el de las transformadas rápidas de Fourier es
mayor, O(N logN). Dicho con otras palabras, el método de Fourier da mayor
precisión en la estimación, pero tarda un mayor tiempo en ejecutar las
operaciones en comparación con el de diferencias finitas básico. Para aumentar
la convergencia del método de diferencias finitas, se pueden aplicar esquemas
de mayor orden, a costa de aumentar los tiempos de ejecución.
Figura
4. Error en el cálculo de la derivada de la función sinc(t) a medida que
aumentamos el número de muestras. En rojo, método de la transformada de
Fourier. En azul, método de diferencias finitas.
Antonio Alex Amor,
Profesor Colaborador Doctor de la Universidad
CEU San Pablo,
Colaborador del Grupo SWAT de la Universidad de
Granada
Referencias
[1] 3Blue1Brown, “Pero ¿qué es la
Transformada de Fourier? Una introducción visual”, https://www.youtube.com/watch?v=spUNpyF58BY
[2] NTI Audio “Transformación rápida de Fourier FFT - Conceptos básicos”
https://www.nti-audio.com/es/servicio/conocimientos/transformacion-rapida-de-fourier-fft
[3]
A. Ramírez-Arroyo, A. Alex-Amor, C. García-García, Á. Palomares-Caballero, P.
Padilla and J. F. Valenzuela-Valdés, "Time-Gating Technique for Recreating
Complex Scenarios in 5G Systems," IEEE Access, vol. 8, pp. 183583-183595,
2020.
[4]
A. Alex-Amor, F. Mesa, Á. Palomares-Caballero, C. Molero and P. Padilla,
"Exploring the Potential of the Multi-Modal Equivalent Circuit Approach
for Stacks of 2-D Aperture Arrays," IEEE Transactions on Antennas and
Propagation, vol. 69, no. 10, pp. 6453-6467, Oct. 2021.
[5]
Steve Brunton, “Solving the Heat Equation with the Fourier Transform”
https://www.youtube.com/watch?v=7haZCrQDHpA&t=597s
[6]
meyavuz, “Collection of FDTD animations [Finite Difference Time Domain]”
https://www.youtube.com/watch?v=AvBsu9ooHcI&t=28s
[7] Wikiversidad, “Propiedades de
la Transformada de Fourier”
https://es.wikiversity.org/wiki/Propiedades_de_la_transformada_de_Fourier#Demostraciones
[8]
H. Sun, Y. Zhang, D. Baleanu, W. Chen, Y. Che, “A new collection of real world
applications of fractional calculus in science and engineering”, Commun.
Nonlinear Sci. Numer. Simulat., vol. 64, pp. 213-231, 2018.
[9]
S. Sengupta, U. Ghosh, S. Sarkar and S. Das, “A Mathematical Approach to
Characterize Left Ventricular Hypertrophy from ECG Diagrams”, Open J.
Cardiol. Heart Dis., 2578-0204, 2018.
[10]
Steve Brunton, “Computing Derivatives with FFT [Matlab]”,
https://www.youtube.com/watch?v=BCexJ-yfdi8
[11]
Steve Brunton, “Computing Derivatives with FFT [Python]”,
https://www.youtube.com/watch?v=y8SqkjoKV4k&t=134s
[12]
Nham Quynh Huong, “W5V5 Solving the 1D/2D Wave Equation with Python -
Computers, Waves, Simulations: A Practical”
https://www.youtube.com/watch?v=LQ4ejGdBjiI&t=238s

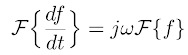










Comentarios
Publicar un comentario